En busca de la partícula de Dios

Los científicos están más cerca que nunca de responder al enigma del llamado bosón de Higgs, según el cual existe una escurridiza partícula que explicaría el comportamiento de las partículas elementales y el origen de la masa, en cuya búsqueda se han invertido grandes esfuerzos y recursos. Representantes de los detectores CMS y ATLAS, del Gran Colisionador de Hadrones (LHC) del Centro Europeo de Investigación Nuclear (CERN) de Ginebra, presentaron ayer los resultados obtenidos este año y que arrojan indicios "intrigantes" de la eventual existencia de la también conocida como la partícula de Dios, considerada crucial para entender la estructura de la materia a nivel subatómico.
Si queréis conocer los resultados, pinchad en este enlace:
http://www.diariodenavarra.es/noticias/mas_actualidad/cultura/la_particula_dios_esta_muy_cerca_58423_1034.html

  Este gráfico del Centro Europeo de Investigación Nuclear muestra los trazos
 dejados por el choque de dos protones.

Impact Earth

Impact Earth es una página interesante donde se pueden comprobar las catástrofes que se producirían si un meteorito chocara contra la Tierra. Los efectos dependerán de la inclinación del meteorito con respecto a la Tierra (grados), del espacio donde impacte y de más cosas que podéis comprobar pinchando en este enlace.
http://www.purdue.edu/IMPACTEARTH


                                   




Ejemplos:
- Meteorito 1.
Diámetro: 400 km
Densidad: 800 kg/m³
Inclinación: 90º
Velocidad: 72 km/s
Profundidad del agua: 1000 m
Distancia: 200 km

Energía: el intervalo promedio entre los impactos de este tamaño es más largo que la edad de la Tierra.
Daños globales: el impacto no hace un cambio notable en la inclinación del eje de la Tierra, aunque pierde una masa despreciable.
Dimensión del cráter: el cráter abierto en el agua tiene un diámetro de 5310 km.


- Meteorito 2.
Diámetro: 3500 km
Densidad: 800 kg/m³
Inclinación: 90º
Velocidad: 72 km/s
Profundidad del agua: 10 m
Distancia: 100 km


Daños globales: la Tierra ha sido destruida por el impacto y sus restos forman un cinturón de asteroides con nueva órbita alrededor del Sol.
Energía el intervalo promedio entre los impactos de este tamaño es más largo que la edad de la Tierra.
Dimensión del cráter: el cráter tiene un diámetro de 28800 km.

El impacto de un meteorito con más de 6 km de diámetro supondría la extinción de la especie.

Vectores

Características de un vector:
- Intensidad.
- Dirección.
- Sentido.
- Punto de aplicación.

Para conocer la dirección y el sentido del cuerpo, hace falta conocer las fuerzas que actúan sobre él.
Supongamos que la M es el cuerpo.
                                                              F.normal
                                                                   ↑
                                         F.rozamiento ←  M → F. motor
                                                                   ↓
                                                                Peso


Si la fuerza de rozamiento es igual a la fuerza motor el cuerpo no se mueve.
La fuerza normal se anula con el peso del cuerpo.

Fórmula de la fuerza de rozamiento:
F.roz = μ x N

Problema resuelto:
Supongamos que el cuerpo está en una mesa.
- Calcula la fuerza neta del cuerpo.            
- Calcula la aceleración.
                                                                 m = 5 kg
                                                       F.roz ← M → 100N
                                                                  μ = 0,5

g aproximádamente = 10 m/s al cuadrado
F roz = 0,5 x 10 x 5 = 25 N -------> Nota: la fuerza normal es la misma que el peso.
                                                                   
                                                                    M → 75N

F = m x a
a = 75/5 = 15 m/s al cuadrado
                                                                   

Las poleas

Nosotros hemos estado trabajando con poleas similares a esta foto, pero en vez de la mano, con un material con una determinada masa.

En esta polea existen diferentes fuerzas:
- Tensión: en este caso la fuerza normal, con dirección hacia arriba. La tensión es la misma en ambos lados.
- El peso: m x g ----> Hay dos pesos: P1  y P2


Para calcular la aceleración y la tensión de la polea hay que resolver el siguiente sistema:
(T - P1 = m1 x a
(P2 - T = m2 x a


Problema resuelto:
m1 = 10 kg
m2 = 50 kg

(T - 10 x 9,81 = 10 x a --------->     T -98,1 = 10 x 6,54
(50 x 9,81 - T = 50 x a                  T= 163,5 N

(T- 98,1 = 10a
(490,5 -T = 50a   ------------->          392,4 = 60a
                                                  a = 392,4/60 = 6,54 m/s al cuadrado
                                           
                                             

Los principios de la dinámica

Primer principio de la dinámica: principio de la inercia.
Todo cuerpo permanece en estado de reposo o en movimiento rectilíneo y uniforme mientras no actúe sobre él una fuerza neta (varias fuerzas pueden estar actuando sobre un cuerpo, pero si la resultante es nula, no hay fuerza neta).

La inercia es la tendencia de un cuerpo a mantener su estado de reposo o de movimiento.






















Una interacción es cualquier mecanismo por el que dos o más cuerpos modifican su estado de reposo o de movimiento. La magnitud que mide cuantitativamente la intensidad de una interacción es la fuerza.



Segundo principio de la dinámica: principio fundamental de la dinámica.
Las fuerzas originan aceleraciones. La relación existente entre las magnitudes de fuerza, masa y aceleración, viene definida por la siguiente ecuación:
F neta = m x a

La aceleración de un cuerpo es proporcional a la fuerza resultante ejercida sobre el mismo, con la misma dirección y sentido que dicha fuerza, e inversamente proporcional a la masa del cuerpo.
a = F/m

Es el ejemplo de las poleas:

Tercer principio de la dinámica: principio de acción y reacción.
Cuando dos cuerpos interaccionan, las fuerzas que ejercen el uno sobre el otro tienen idéntico módulo y dirección, pero sentidos opuestos.
El tercer principio de la dinámica describe una propiedad importante de las fuerzas: siempre se presentan en parejas.
Las fuerzas de acción y reacción nunca se anulan entre sí, debido a que actúan sobre cuerpos diferentes.

La ley de Hooke

Un muelle constituye un ejemplo típico de cuerpo elástico. Si lo estiramos se alarga, y si lo soltamos recupera su longitud inicial. Existe una relación cuantitativa existente entre la fuerza aplicada y la deformación producida.

Ley de Hooke: la deformación de un cuerpo elástico es directamente proporcional a la fuerza que la produce.
F = fuerza (N)
K = constante elástica del muelle (N/m)
Δ/ = alargamiento (m)

Fórmula:  F = k x Δ/

La constante elástica del muelle (k) se puede hallar de tres maneras diferentes, que están visibles en esta práctica:
Hallar la k del muelle

Tema 2: Interacciones entre los cuerpos

Para entender este tema lo primero que hay que saber es qué es la fuerza. La fuerza es toda causa capaz de modificar el estado de reposo o de movimiento de un cuerpo o de producir una deformación en él. La unidad de fuerza en el SI es el newton, N.
Cada material responde de una forma diferente a la acción de las fuerzas y podemos clasificarlos en:
- Rígidos: no modifican su forma cuando actúa sobre ellos una fuerza. Un material rígido es la madera.

- Elásticos: recuperan su forma original cuando deja de actuar la fuerza que los deforma. Una goma es un material elástico.












- Plásticos: al cesar la fuerza que los deforma, los materiales no recuperan su forma primitiva y quedan deformados permanentemente. La plastilina es un material plástico.












Los cuatro puntos principales de este tema son:
- La ley de Hooke
- Las tres leyes de Newton: los principios de la dinámica
- Vectores
- Las poleas

El mismísimo Newton

Sir Isaac Newton (25 de diciembre de 1642, Woolsthorpe, Lincolnshire, Inglaterra- 20 de marzo de 1727, Kensington, Londres, Inglaterra) fue un físico, filósofo, teólogo, inventor, alquimista y matemático inglés, autor de los Philosophiae naturalis principa mathematica, más conocido como los Principa donde describió la ley de gravitación universal y estableció la base de la mecánica clásica mediante las leyes que llevan su nombre. Entre sus otros descubrimientos científicos destacan los trabajos sobre la naturaleza de la luz y la óptica (que se presentan principalmente en su obra Opticks) y el desarrollo del cálculo matemático.

Esto es, prácticamente, una milésima parte de la vida de Newton; si queréis conocer más sobre él podéis pinchar en estos enlaces:
http://es.wikipedia.org/wiki/Isaac_Newton
http://www.biografiasyvidas.com/biografia/n/newton.htm
http://thales.cica.es/rd/Recursos/rd97/Biografias/03-1-b-newton.html

El mayor científico de todos los tiempos, reconocido por Einstein e incluyéndose a  él.

Epitafio de Newton:
Aquí descansa SIR ISAAC NEWTON, Caballero que con fuerza mental casi divina demostró el primero, con su resplandeciente matemática, los movimientos y figuras de los planetas, los senderos de los cometas y el flujo y reflujo de los océanos. Investigó cuidadosamente las diferentes refrangibilidades de los rayos de luz y las propiedades de los colores originados por aquellos. Intérprete, laborioso, lagaz y fiel de la Naturaleza, Antigüedad, y de la Santa Escritura, defendió en su Filosofía la Majestad del Todopoderoso y manifestó en su conducta la sencillez del evangelio.
Dad las gracias, mortales, al que ha existido así, y tan grandemente como adorno de la raza humana. Nació el 25 de diciembre de 1642; falleció el 20 de marzo de 1727.

Práctica para hallar la constante de un muelle

m(kg)	ΔX(m)	F(N)
0	0	0
0,1	0,05	0,981
0,2	0,08	1,962
0,3	0,17	2,943
0,4	0,22	3,924
0,5	0,25	4,905
0,6	0,33	5,886
0,7	0,36	6,867
0,8	0,42	7,848

1ª forma: a mano

Representar los puntos en una gráfica, en el eje "y" la F y en el eje "x" la ΔX.

Como lo que hay que representar es la fuerza y no la masa se multiplica la masa por 10 (aproximación de la gravedad). F=m x g

Para hallar la constante se hace una recta cercana a todos los puntos. Hay una ley que dice que:

m (pendiente)= (y 2  - y 1) / (x 2 - x 1)

En este caso la pendiente es la k (constante del muelle), por lo que hay que coger dos puntos que pasen por la recta y aplicarle esta fórmula. Contra más alejados estén los puntos mayor exactitud habrá.

K= (7,848-0)/(0,42-0)= 18,68 N/m --------> Se pone cero porque es un punto que pasa por la recta.

2ª forma: a ordenador

3ª forma

Hay que representar los puntos en la gráfica, como en la primera forma, pero esta vez a escala. 

Después, con un transportador de ángulos, calcular el ángulo de la recta con respecto al eje x.

Pendiente de la recta= tangente de el nº de grados.

A mí me ha dado 63,5 grados -----> pendiente de la recta=tan de 63,5=2,005N/dm

Las medidas están representadas en decímetros porque si no no me hubiera cupido en el cuaderno, por lo que se pasa a metros.

K= 20,05 N7m

Para hallar la K final, hay que hallar la media de las tres formas:

(20,05+18,68+18,312)/3=19,014 N/m

Premios Nobel Física y Química 2011

Nobel de Física para la aceleración del universo
Los científicos Saul Perlmutter, Brian Schmidt y Adam Riess, reciben el Priemo Nobel de Física 2011 por sus observaciones cosmológicas, al descubrir que la expansión del universo, el Big Ban, está acelerándose, según ha informado el comité Nobel de Física de la Real Academia de Ciencias Sueca. Es un fenómeno que los científicos no han logrado aún explicar pero se ha comprobado en diferentes observaciones realizadas después de los trabajos pioneros de los tres galardonados, hace más de una década. Es el misterio de la energía oscura del universo y la mejor interpretación, según muchos expertos, es la constante cosmológica de Einstein. Perlmutter y Riess trabajan en EE.UU y Schmidt, en Australia. Su hallazgo tiene implicaciones directas en el destino del universo, ya que esa aceleración de la expansión indica que el cosmos acabará completamente helado.

Adam Riess, Saul Perlmutter y Brian Schmidt.

Si quieres saber más sobre este artículo, pinche en estos dos enlaces:
http://www.elpais.com/articulo/sociedad/Nobel/Fisica/aceleracion/universo/elpepusoccie/20111004elpepusoc_4/Tes
http://francisthemulenews.wordpress.com/2011/10/04/premio-nobel-de-fisica-2011-la-energia-oscura-y-la-expansion-acelerada-del-espaciotiempo/


Nobel de Química para los cuasicristales
Daniel Shechtman, científico del Instituto de Tecnología de Haifa (Israel), recibe este año el Premio Nobel de Química, en solitario, por el descubrimiento de los cuasicristales, según ha anunciado la Real Academia de Ciencias Sueca.
"En los cuasicristales encontramos los fascinantes mosaicos del mundo árabe reproducidos al nivel de átomos: partrones regulares que nunca se repiten a sí mismos", explica la Academia Sueca. "Sin embargo, la configuración descubierta en los cuasicristales se consideraba imposible y Shechtman tuvo que luchar una dura batalla contra la ciencia establecida", añaden los académicos. El hoy trabajo premiado alteró fundamentalmente la concepción de los químicos acerca de la materia sólida.

Daniel Shechtman

Si te ha interesado la noticia y quieres conocer más, pincha en este enlace:
http://www.elpais.com/articulo/sociedad/Nobel/Quimica/2011/cuasicristales/elpepusoccie/20111005elpepusoc_6/Tes

Práctica:cómo hallar la gravedad

Nosotros, los alumnos de 4º ESO, hemos hallado la gravedad que hay desde el segundo piso del colegio hasta el patio, utilizando únicamente materiales cotidianos.
Para realizar esta práctica hemos necesitado:
- Tres pelotas de balonmano
- Un cronómetro
- Un palo largo
- Un palo corto
Para empezar, hemos tenido que hallar la altura del 2º piso y, ¿cómo lo hemos hecho?:
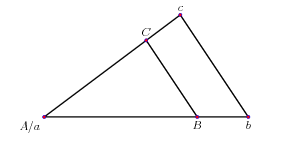
En el patio, hemos colocado los palos (primero el corto y luego el largo) de tal manera que mirando desde la altura del palo corto en dirección diagonal, coincida a su vez con la altura del palo largo y con la altura del segundo piso. Pensaréis que es una cosa demasiado extraña, pero no. Esa diagonal es la hipotenusa del triángulo de tales, y la distancia que hay entre el palo corto y la pared, es uno de los catetos. Nos falta hallar el otro cateto, que es la altura del 2º piso.

A= palo corto (1m)
C= altura del palo largo (2,53m)
c= altura del 2º piso (8,75 + palo corto)
a-B= distancia palo corto-palo largo (2,08m)
B-b= distancia palo largo- pared del patio (9,82m)
a-B= distancia palo corto- pared del patio (11,9m)
A-C= distancia altura palo corto-altura palo largo (2,57m)
C-c= distancia altura palo largo- altura segundo piso (12,13m)
A-c= distancia altura palo corto-altura 2º piso (14,70m)
Razón de semejanza= 5,72
A la altura del 2º piso que es 8,75 (cateto) hay que sumarle 1 metro, la altura del palo corto.
Altura 2º piso = 9,75m


Esta altura nos ha dado a un compañero mío y a mí.
Altura media de la clase 2º piso: 10,18m


Después, nuestro fantástico delegado Óscar ha tenido que tirar tres pelotas y nosotros hemos tenido que calcular con el cronómetro el tiempo tarda en llegar al suelo cada pelota.
El tiempo medio que nos ha dado a toda la clase es de 1,23s.

Fórmula gravedad: g= (2 x Xf) / t ( al cuadrado)
g = 13,46
Comparando la gravedad que nos ha dado con la que dijo Galileo Galilei, nos ha dado un porcentaje de error de 37%.
Un porcentaje de error muy alto debido a:
- La diferencia de reflejos entre las personas de la clase para calcular el tiempo.
- Lo que tarda en escuchar Óscar la señal del profesor para que lance la pelota.
- Lo que nosotros tardamos en escuchar el bote de la pelota.
- La mala colocación de los palos para calcular la altura.

Movimiento de caída libre

Galileo Galilei fue el primero en demostrar experimentalmente que, si se desprecia la resistencia que ofrece el aire, todos los cuerpos, independientemente de cuál sea su masa, caen hacia la Tierra con la misma aceleración, la de la gravedad: g = 9,8 m/s(al cuadrado). Este movimiento pertenece al MRUA, ya que la aceleración en este caso es "g".
Fórmulas:
- V = G x T
- Xf = 1/2 G x T (al cuadrado).

En el siguiente vídeo se muestra la comprobación de la teoría de Galileo.

MRUR (Movimiento Rectilíneo Uniformemente Retardado)

El movimiento rectilíneo uniformemente retardado es aquel movimiento rectilíneo cuya aceleración es negativa, de modo que la velocidad disminuye con el tiempo.
Las fórmulas son las mismas que en los MRUA, pero hay que fijarse en que la aceleración es negativa.
- Xf = Xi + V x T + 1/2 a x T (al cuadradro)
- a = (Vf - Vi) / T
- Vf = Vi + a x T

Gráfica espacio-tiempo
  -
- El movimiento describe una parábola invertida, debido a que la aceleración es negativa.









- Al ser la aceleración negativa, la velocidad disminuye conforme pasa el tiempo.

MRUA (Movimiento Rectilíneo Uniformemente Acelerado)

En este tipo de movimiento, la velocidad aumenta conforme transcurre el tiempo, es decir, que la velocidad no es constante.
El símbolo de la aceleración es la "a" y se representa en m/s(al cuadrado)

Fórmulas:

- Xf = Xi + Vi x T + 1/2 a x T al cuadrado

- a = (Vf-Vi)/ T

- Vf = Vi + a x T

Gráfica espacio-tiempo       
                                                                                                                                                          

- Se trata de una parábola, puesto que el espacio y el tiempo no son directamente proporcionales. Conforme transcurre el tiempo, el espacio recorrido no aumenta siempre en la misma medida, sino que crece más deprisa

      

Gráfica velocidad-tiempo

- La pendiente de la recta es positiva, y su valor coincide con el de la aceleración.

- La recta no pasa por el origen de coordenadas, ya que en instante inicial la velocidad es de 2 m/s.

MRU (Movimiento Rectilíneo Uniforme)

Se caracteriza por tener una trayectoria rectilínea y una velocidad cuyo módulo, dirección y sentido permanecen constantes en el tiempo. Por tanto, es un movimiento en el que la aceleración es nula.
Fórmulas:
- Punto final= punto inicial + velocidad x tiempo- - - - - > Xf = Xi + V x T
- AX= espacio recorrido -----> Xf-Xi


Gráfica espacio-tiempo

- Al ser la velocidad constante, el móvil recorre espacios iguales en tiempos iguales.

- Se trata de una línea recta cuya pendiente es el valor de la velocidad del móvil.

Gráfica velocidad-tiempo     

      

      

- La línea es recta y horizontal, porque la velocidad es constante. 

Tema 1: Estudio del movimiento

Para describir el movimiento de un cuerpo necesitamos un sistema de referencia , que generalemente es el sistema cartesiano de coordenadas.

Para entender bien este tema hay que tener claros estos conceptos:

- Trayectoria: es la línea imaginaria que describe un cuerpo al desplazarse. Esta línea la forman las posiciones por las que ha pasado el cuerpo en su movimiento.

- Espacio recorrido: la distancia recorrida por el móvil sobre la trayectoria.

- Desplazamiento: la diferencia de posición que ocupa un cuerpo entre dos instantes de tiempo considerados. Se expresa en metros.
- Velocidad: es la rapidez con que cambia de posición un cuerpo
- Velocidad media: es el desplazamiento efectuado por un cuerpo en la unidad de tiempo.
- Velocidad instantánea: es la velocidad de un cuerpo o móvil en cada instante o en un determinado punto de trayectoria.
- Aceleración: es la rapidez con que varía la velocidad de un cuerpo.

Según su trayectoria podemos clasificar los móviles en: rectilíneos (línea recta), curvilíneos (línea curva) y circular (circunferencia).

                                                         

Movimiento rectilíneo

Movimiento curvilíneo

          

            Movimiento circular

Nosotros en este tema hemos estudiado los movimientos rectilíneos entre los que se encuentran:

-MRU (Movimiento Rectilíneo Uniforme)

-MRUA (Movimiento Rectilíneo Uniformemente Acelerado). Dentro de estos movimientos se encuentra el  movimiento de caída libre.

-MRUR (Movimiento Rectilíneo Uniformemente Retardado)

¿Los neutrinos más rápidos que la luz?

Unos científicos logran unas medidas controvertidas en el laboratorio italiano de Gran Sasso. Los rumores corren ya hace unos días porque lo que estos científicos plantean es que han medido neutrinos (partículas elementales de escasa masa y que apenas interaccionan con la materia) que, aparentemente, se desplazan más rápido que la luz. De confirmarse, sería un bombazo en la física, puesto que es un pilar de la teoría de Einstein que nada puede superar la velocidad de la luz.

Si te interesa este tema puedes saber más en estas páginas:

http://www.elpais.com/articulo/sociedad/Neutrinos/rapidos/luz/elpepusoc/20110922elpepusoc_10/Tes

http://www.publico.es/ciencias/398042/el-neutrino-desafia-a-einstein